用高中数学比较深度地学习吉他乐理

work with ChatGPT

吐槽一下，mdx屁事好多😅

求吉他弦的幅度谱

我们一步步来，从最简单的概念出发，最终得到吉他弦的幅度谱。

什么是幅度谱

吉他弦振动时，不是只发出一个单独的音，而是同时包含基音（主音高）和泛音（谐波）。

幅度谱（Amplitude Spectrum）告诉我们：

每个频率成分的振幅
哪些频率的声音最强，哪些较弱

你可以把它想象成：

低音吉他可能主要有低频峰值
电吉他可能会有更多的高频泛音
不同吉他、不同拨弦方式的幅度谱不同

所以，我们的目标是：找出吉他弦振动中不同频率的振幅！

吉他弦的振动是什么样的？

当你拨动吉他弦时，它的振动可以用数学上的正弦波来表示。

如果弦长是 $L$ ，那么它的振动模式（忽略阻尼）可以写成：

$u(x,t) = A_1 \cos(\omega_1 t) \sin\left(\frac{\pi x}{L} \right) + A_2 \cos(\omega_2 t) \sin\left(\frac{2\pi x}{L} \right) + \dots$

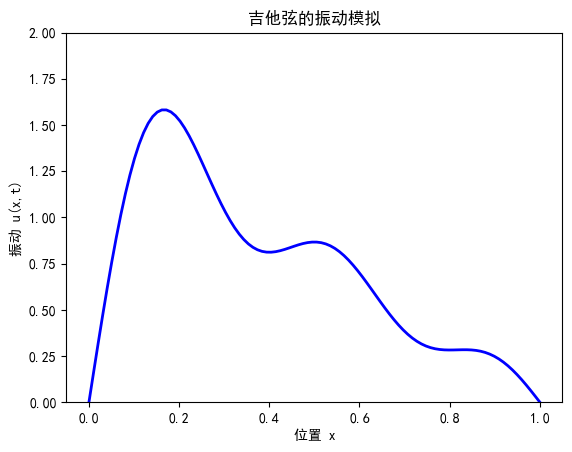
公式描述的是吉他弦的振动模式，也就是弦在某个位置 𝑥 处，随着时间 𝑡 的振动情况

这意味着：

不同频率的正弦波叠加形成吉他弦的振动
每个频率对应一个振幅 $A_n$
这些振幅就是我们要找的“幅度谱”

而这里的频率 $f_n$ 是固定的：

$f_n = \frac{n v}{2L}, \quad n = 1,2,3,\dots$

其中：

$n = 1$ 叫基频，决定了吉他的音高
$n = 2,3,4,\dots$ 叫泛音，影响音色

用傅里叶分析找出每个频率的振幅

傅里叶分解

数学上，我们可以使用傅里叶级数把任意复杂的周期振动写成一堆正弦波的叠加：

$u(t) = A_1 \cos(\omega_1 t) + A_2 \cos(\omega_2 t) + A_3 \cos(\omega_3 t) + \dots$

现在，我们的问题就变成：

如何找到每个 $A_n$ ？
$A_n$ 就是幅度谱的值！

计算振幅 $A_n$

数学上，振幅 $A_n$ 由下面的积分计算：

$A_n = \frac{2}{T} \int_0^T u(t) \cos(\omega_n t) dt$

这告诉我们：

如果想知道某个频率的振幅，就把 $u(t)$ 乘上那个频率的正弦波并积分
这样可以提取出那个特定频率的“强度”

你可以把这个过程想象成：

你在一首歌里想找到某个鼓点的声音
你可以用耳朵“滤掉”别的声音，专注听这个鼓点的节奏
数学上的积分就是在做“滤波”：只留下某个频率的成分

画出幅度谱

计算出每个 $A_n$ 以后，我们可以画出幅度谱：

横轴：频率（Hz）
纵轴：振幅 $A_n$
只有某些特定频率有振幅（因为吉他弦的振动是离散的）
这张图可以直观展示吉他弦音色的特点

如果我们得到：

频率 (Hz)	振幅 $A_n$
110 Hz	1.0
220 Hz	0.5
330 Hz	0.3

那么画出的幅度谱可能是这样：

这说明：

110Hz 是最强的（基频，主音）
220Hz、330Hz 也是有的，但更弱（泛音，决定音色）

十二平均律

十二平均律是一种等比的音阶系统，它把一个八度（2 倍频率）等分成 12 个音。音名分别是: C, C#/C♭, D, D#/E♭, E, F, F#/G♭, G, G#/A♭, A, A#/B♭, B, 在钢琴上重复，分布如下：

从幅度谱到音高

音高（Pitch） 由基频（fundamental frequency, $f_1$ ） 决定，而音色（Timbre） 由泛音（Overtones, $2f_1, 3f_1, 4f_1, ...$ ） 影响。

举个例子：

假设你弹吉他 110Hz（A2）这一音
频谱上可能有：
- 110Hz（基频） → 主要音高
- 220Hz（第二谐波）
- 330Hz（第三谐波）
- 440Hz（第四谐波）
- 这些谐波会影响音色，但音高仍由基频 110Hz 决定。

如果你想换成 A3（220Hz），你会发现：

220Hz 仍然符合谐波的整数倍规律
但你并不会直接弹 220Hz，而是弹 110Hz 的“下一个 A”。这背后就是音阶系统的作用！

音乐音阶和频率的关系

音乐音阶和频率是指数关系。

在自然泛音序列中：

$f_n = n f_1$

所有谐波都是整数倍，但自然泛音和我们常用的音阶不完全匹配！所以人类为了让乐器方便演奏，就发明了音阶（scales）。

为什么用 12 个音

人耳听觉是“对数感知”的，即 频率间隔是等比关系，不是等差关系。
如果用“等倍频率”的音阶，每个八度都和谐，但音程会不均匀。
十二平均律的核心：每个音高是前一个音高的 12 次方根比率。

公式：

$f_n = f_0 \times (2^{1/12})^n$

其中：

$f_0$ 是参考音高（如 A4 = 440Hz）
每个音 $f_n$ 是上一个音的 $2^{1/12}$ 倍
每升高 12 个半音，频率翻倍！

例如，从 A4（440Hz）出发：

A#4 = $440 \times 2^{1/12}$ ≈ 466Hz
B4 = $440 \times 2^{2/12}$ ≈ 494Hz
C5 = $440 \times 2^{3/12}$ ≈ 523Hz
……
A5 = $440 \times 2^{12/12}$ = 880Hz（正好 2 倍）

所以，我们人为构造了一个“等比”音阶，使得任何调性都可以被公平使用。

频谱上如何看到十二平均律

如果你对吉他、钢琴的声音做傅里叶变换，你会发现：

基频决定音高（如 A = 110Hz）
但不同乐器，谐波的强度分布不同，导致音色变化
如果你在一个平均律乐器（如钢琴、电子合成器）上弹音阶，傅里叶变换会显示每个音高按 $2^{1/12}$ 递增！

假设你弹奏 440Hz（A4）和 494Hz（B4），你会看到：

峰值分别出现在 440Hz 和 494Hz
频率比是： $frac{494}{440} \approx 2^{2/12} \approx 1.122$ 这个比值正好是十二平均律中的音程比率！

wip，所有涉及绘图的代码详见 https://github.com/nick-cjyx9/ilesBlog/blob/main/src/pages/post/guitar.ipynb